Metoda Newtona
Metoda Newtona (czasami też zwana metodą Newtona-Raphsona) służy do rozwiązywania równań nieliniowych. Dla przykładu zastanówmy się jak obliczyć pierwiastek z danej liczby $\sqrt{c}$.
$$x_{i+1} = \cfrac{1}{2}\left(x_i + \cfrac{c}{x_i}\right)$$Sprawdźmy czy dany wzór działa na przykładzie wyznaczania pierwiastka kwadratowego z liczby $c=3$. Aby to zrobić poczebujemy pewnego punktu startowego $x_0$ - czyli naszego pierwszego oszacowania ile wynosi wartość takiego pierwiastka. Dajmy na to, że zupełnie nie wiemy ile on wynosi i przyjmujemy $x_0=5$.
$$i=0, \quad x_{1} = \cfrac{1}{2}\left(x_0 + \cfrac{3}{x_0}\right) = \cfrac{1}{2}\left(5.00 +\cfrac{3}{5.00}\right)=2.80$$ $$i=1, \quad x_{2} = \cfrac{1}{2}\left(x_1 + \cfrac{3}{x_1}\right) = \cfrac{1}{2}\left(2.80 +\cfrac{3}{2.80}\right)=1.96$$ $$i=2, \quad x_{3} = \cfrac{1}{2}\left(x_2 + \cfrac{3}{x_2}\right) = \cfrac{1}{2}\left(1.96 +\cfrac{3}{1.96}\right)=1.74$$Wraz z kolejnymi iteracjami dostajemy coraz lepsze oszacowanie, które wynosi $\sqrt{3} = 1.732050807568872...$. Nawet gdy nasz punkt startowy będzie daleko od dokładnej wartości metoda Newtona bardzo szybko będzie zbiegać do poprawnej wartości. Mówimy że metoda ta ma kwadratową zbieżność. Zestawmy otrzymane wyniki w tabeli
| iteracja | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| $x_0=5$ | 5 | 2.8 | 1.94 | 1.743 | 1.7321 | 1.73205 | 1.7320508075 |
| $x_0=500$ | 250 | 125 | 62.51 | 31.28 | 15.68 | 7.94 | 4.15 |
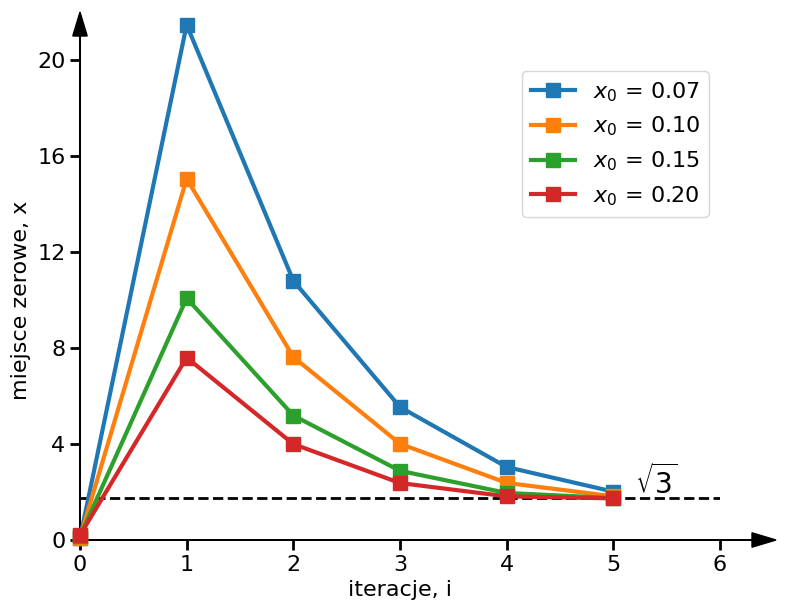
Na poniższym wykresie zobrazowane zostały kolejne iteracje metody Newtona w zależności od przyjętego punktu startowego.
Skoro jak pokazano wzór na obliczanie pierwiastka działa, to pokażmy skąd ten wzór się bierze. Rozwińmy więc funkcje $f(x)$ w szereg Taylora
$$f(x+h) = f(x) + \cfrac{1}{1!}\cfrac{df(x)}{dx}h + \cfrac{1}{2!}\cfrac{d^2f(x)}{dx^2}h^2 + ...+\cfrac{1}{n!}\cfrac{d^nf(x)}{dx^n}h^n,$$gdzie $h$ jest pewnym punktem z otoczenia $x$. Zostawiając tylko pierwsze dwa człony otrzymujemy
$$f(x+h) \approx f(x) + \cfrac{df(x)}{dx}h.$$Chcemy znaleźć miejsce zerowe tej funkcji a więc rozważamy równanie $f(x+h) = 0$. Podstawiając do wzoru $x = x_i$ oraz $h = x_{i+1} - x_i$ dostajemy
$$0 = f(x_i) + f^{'}(x_i)(x_{i+1} - x_i)$$Po drobnych przekształceniach otrzymujemy wzór na $x_{i+1}$
$$x_{i+1} = x_i - \cfrac{f(x_i)}{f^{'}(x_i)}.$$Przyjmując za funkcja $f(x) = x^2-c$ i poszukując jej miejsca zerowego dostaniemy wynik $\pm\sqrt{c}$. Stosując do tego zagadnienia metodę Newtona musimy w pierwszej kolejności obliczyć pochodną funkcji $f(x)$. Pochodna ta jest równa $f^{'}(x) = 2x$. Wykorzystujac wzór metody Newtona dostajemy
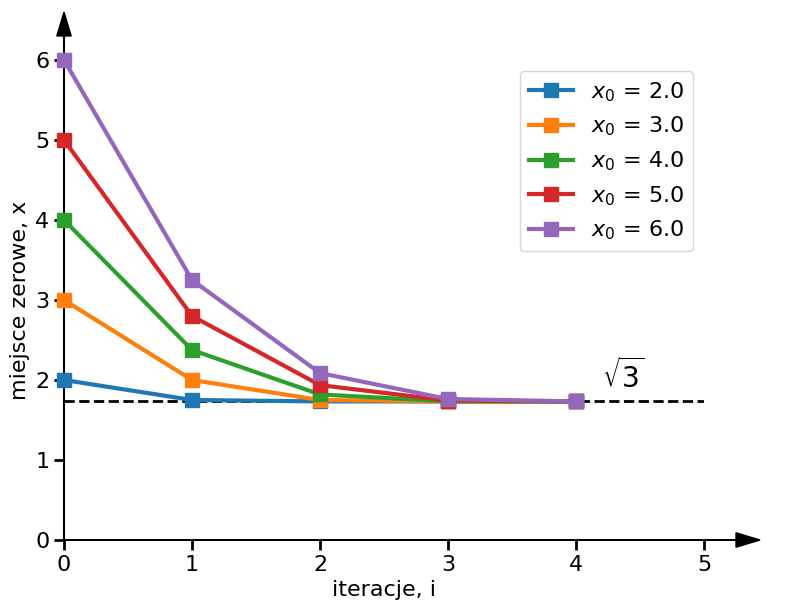
$$x_{i+1} = x_i - \cfrac{x_i^2-c}{2x_i} = x_i -\cfrac{1}{2}x_i + \cfrac{1}{2}\cfrac{c}{x_i} = \cfrac{1}{2}x_i + \cfrac{1}{2}\cfrac{c}{x_i} = \cfrac{1}{2}\left(x_i + \cfrac{c}{x_i}\right)$$Poniżej zaprezentowany jest wykres zbieżności metody Newton dla punktów startowych w pobliżu $0$.